Mechanics and behavior of Metals, also known as the mechanics of materials, is a branch of mechanics that studies the behavior of solid materials under various forms of loading. This field is crucial in engineering because it helps to predict how materials will deform, break, or otherwise react under different conditions.

Here are some key concepts:

1. Stress and Strain

Stress is the force applied to a material per unit area, while strain is the resulting deformation or change in shape of the material. Stress and strain are important concepts in engineering and materials science.

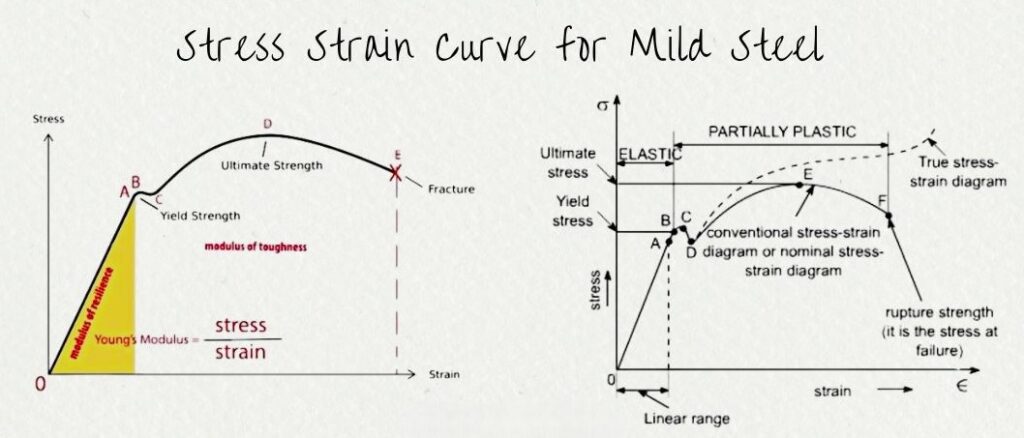
• Stress: The internal forces per unit area within a material. It is typically measured in Pascals (Pa) or pounds per square inch (psi).
  • Normal Stress (𝜎): Acts perpendicular to the surface.

𝜎 = 𝐹/𝐴​

• Shear Stress (𝜏): Acts parallel to the surface.

𝜏 = 𝐹/𝐴​

• Strain: The deformation of a material relative to its original length.
  • Normal Strain (𝜖): Change in length per unit length.

𝜖 = Δ𝐿/𝐿​

• Shear Strain (𝛾): Angular deformation.

2. Elasticity and Plasticity

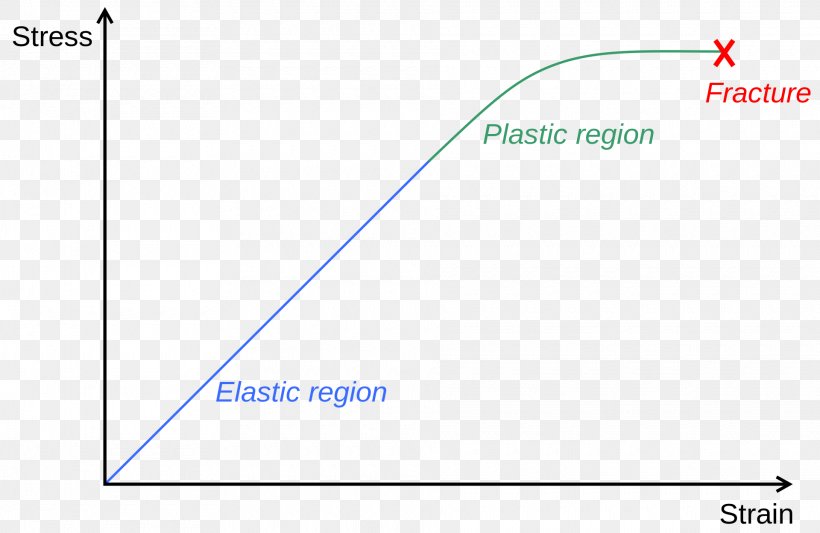
• Elasticity: The property of a material to return to its original shape after the load is removed. Described by Hooke’s Law (𝜎=𝐸𝜖), where 𝐸 is the modulus of elasticity (Young’s Modulus).
• Plasticity: The property of a material to undergo permanent deformation after the yield point is reached.

3. Modulus of Elasticity

• Young’s Modulus (E): Measures stiffness in tension or compression.
• Shear Modulus (G): Measures stiffness in shear.
• Bulk Modulus (K): Measures stiffness under uniform pressure.

4. Poisson’s Ratio (𝜈)

• The ratio of transverse strain to axial strain. When a material is stretched, it tends to get thinner in the perpendicular direction.

5. Failure Theories

• Yield Criteria: Conditions under which a material begins to deform plastically.
  • Von Mises Criterion: Based on the distortion energy theory.
  • Tresca Criterion: Based on the maximum shear stress theory.
• Fracture Mechanics: Study of crack propagation in materials.
  • Stress Intensity Factor (K): Determines the stress state near the tip of a crack.
  • Fracture Toughness (K_IC): A material property indicating resistance to fracture.

6. Fatigue and Creep

• Fatigue: Failure under repeated or fluctuating loads. Characterized by S-N curves (stress vs. number of cycles).
• Creep: Slow, time-dependent deformation under constant stress, significant at high temperatures.

7. Composite Materials

• Materials made from two or more constituent materials with different physical or chemical properties.
  • Matrix and Reinforcement: Typically consists of a matrix (binder) and reinforcement (fibres, particles).
  • Anisotropy: Direction-dependent properties.

8. Material Toughness and Hardness

• Toughness: Ability to absorb energy and plastically deform without fracturing.
• Hardness: Resistance to deformation or indentation, measured by scales such as Mohs, Rockwell, or Brinell.

9. Thermal Effects

• Materials can expand or contract with temperature changes, described by the coefficient of thermal expansion.
• Thermal stresses occur due to temperature gradients within a material.

Applications:

• Structural Engineering: Designing buildings, bridges, and other structures.
• Mechanical Engineering: Designing machinery and components.
• Aerospace Engineering: Designing aircraft and spacecraft structures.
• Materials Science: Developing new materials with specific mechanical properties.

Normal Stress and Shear Stress

Normal Stress

Normal stress is the stress component perpendicular to the surface of a material. It is calculated by dividing the force applied perpendicular to the surface by the area over which the force is distributed. Normal stress can be tensile (pulling apart) or compressive (pushing together).

Formula:

𝜎 = 𝐹/𝐴

 where:

• 𝜎 = Normal stress (Pa or psi)
• 𝐹 = Force applied perpendicular to the surface (N or lb)
• 𝐴 = Cross-sectional area over which the force is applied (m² or in²)

Example: Consider a cylindrical rod with a cross-sectional area of 0.01 m22 subjected to a tensile force of 1000 N.

𝜎 = 1000 N / 0.01 m²

    = 100,000 Pa (or 100 kPa)

Shear Stress

Shear stress is the stress component parallel to the surface of a material. It is calculated by dividing the force applied parallel to the surface by the area over which the force is distributed.

Formula:

𝜏 = 𝐹/𝐴

where:

• 𝜏 = Shear stress (Pa or psi)
• 𝐹 = Force applied parallel to the surface (N or lb)
• 𝐴 = Cross-sectional area over which the force is applied (m² or in²)

Example: Consider a square steel plate with an area of 0.05 m² subjected to a shear force of 200 N.

𝜏 = 200 N / 0.05 m²

    =4,000 Pa

Detailed Example

Let’s consider a more detailed example where both normal stress and shear stress are involved.

Scenario: A rectangular block of material with a height ℎ, width 𝑤w, and depth 𝑑d is subjected to a vertical force and a horizontal force on its top surface. The top surface area 𝐴 is 𝑤×𝑑.

• Given:
  • Vertical force 𝐹𝑣=500 N
  • Horizontal force 𝐹ℎ=300 N
  • Width 𝑤=0.1 m
  • Depth 𝑑=0.05 m

Step 1: Calculate the cross-sectional area:

𝐴 = 𝑤×𝑑

    = 0.1 m × 0.05 m

     = 0.005 m²

Step 2: Calculate the normal stress:

𝜎 = 𝐹𝑣 / 𝐴

=500 N / 0.005 m²

=100,000 Pa

Step 3: Calculate the shear stress:

𝜏 = 𝐹ℎ / 𝐴

   =300 N / 0.005 m²

   =60,000 Pa

Summary

In this scenario:

• The normal stress on the material is 100,000 Pa due to the vertical force.
• The shear stress on the material is 60,000 Pa due to the horizontal force.

Understanding how to calculate and differentiate between normal and shear stress helps in analysing how materials will respond to different types of loading, which is essential for designing safe and efficient structures.

Elasticity and Plasticity

Elasticity

Elasticity is the property of a material that allows it to return to its original shape and size after the forces causing deformation are removed. Materials that exhibit elasticity deform when subjected to stress but recover their original configuration upon unloading. This behaviour is governed by Hooke’s Law within the elastic limit.

Hooke’s Law:

𝜎 = 𝐸 x 𝜖

where:

• 𝜎 = Stress (Pa or psi)
• 𝐸 = Modulus of elasticity (Young’s Modulus) (Pa or psi)
• 𝜖 = Strain (dimensionless)

Example:

Consider a steel rod with a Young’s Modulus 𝐸 of 200 GPa (200 ×10⁹ Pa). If a tensile stress of 400 MPa (400 x10⁶ Pa) is applied, the strain (𝜖) can be calculated as follows:

𝜖 = 𝜎/𝐸

=  (400 x10⁶Pa) / (200 ×10⁹Pa)

=0.002

This strain indicates that the steel rod will elongate by 0.2% of its original length under this stress, and it will return to its original length when the stress is removed, assuming the stress does not exceed the elastic limit.

Plasticity

Plasticity is the property of a material that enables it to undergo permanent deformation after the yield point is surpassed. Unlike elastic deformation, plastic deformation is irreversible. When the stress exceeds a material’s yield strength, it enters the plastic region, where it deforms permanently.

Yield Strength (𝜎𝑦​): The stress at which a material begins to deform plastically.

Example: Consider the same steel rod with a yield strength of 250 MPa. If a tensile stress of 300 MPa is applied:

1. Elastic Deformation (Up to Yield Strength):
   • Up to 250 MPa, the rod behaves elastically.

Strain in elastic region:

𝜖𝑒 =  (250 x 10⁶Pa) / (200 ×10⁹ Pa)

     = 0.00125

2. Plastic Deformation (Beyond Yield Strength):
   • Beyond 250 MPa, the rod deforms plastically.
   • Total strain at 300 MPa includes both elastic and plastic strain.

Elastic strain:

𝜖𝑒 =  (250 x 10⁶Pa) / (200 x 10⁹Pa)

     = 0.00125

Plastic strain:  𝜖𝑝​ (additional permanent deformation)

                          𝜖𝑝 = 𝜖𝑡 – 𝜖𝑒

Total strain:    𝜖𝑡 = 𝜖𝑒+𝜖𝑝 ​

Calculation in Practice

Elastic Region Calculation

• Material: Aluminum with 𝐸=70 GPa
• Stress Applied: 𝜎=140 MPa

𝜖 = 𝜎 / 𝐸

                =(140 x 10⁶Pa) / (70 x 10⁹Pa)

                  ​=0.002

Here, the aluminum deforms elastically, elongating by 0.2% of its original length, and returns to its original length when unloaded.

Plastic Region Calculation

• Material: Copper with 𝐸 = 110 GPa and 𝜎𝑦 = 70 MPa
• Stress Applied: 𝜎 = 100 MPa

1. Elastic Strain:  ϵe​ =  (110×10⁹Pa) / (70×10⁶Pa)

𝜖𝑒 =  0.000636

2. Total Strain (at 100 MPa):   𝜖𝑡 = (100×10⁶Pa) / (110×10⁹Pa)

𝜖𝑡 = 0.000909

3. Plastic Strain:  𝜖𝑝 = 𝜖𝑡−𝜖𝑒

𝜖𝑝 = 0.000909 − 0.000636         

𝜖𝑝 = 0.000273

This means the copper will have a permanent strain of 0.0273% of its original length after the stress is removed.

Summary

• Elasticity: Temporary deformation that returns to the original shape upon unloading. Governed by Hooke’s Law.

Plasticity: Permanent deformation that does not return to the original shape after the stress exceeds the yield strength.

Tags: Hot Rolling Mill, Meta TechX, Meta TechX Engineers, Steel Industry, Steel making